高数II（一）

求分界点、不连续点处的函数偏导数可以使用定义：

设\(z=f(x,y)=\sqrt{|xy|}\)，求\(f_{x}(0,0)\)和\(f_y(0,0)\)

解： \[ \begin{aligned} & f_x(0, 0)=\lim _{x \rightarrow 0} \frac{\sqrt{|x \cdot 0|}-0}{x}=0 \\ & f_y(0,0)=\lim _{y \rightarrow 0} \frac{\sqrt{|y \cdot 0|}-0}{y}=0 \end{aligned} \]

固定一个变量，让另一个趋于所给的值。

\[ f(x, y)= \begin{cases}\dfrac{x y}{x^2+y^2}, & x^2+y^2 \neq 0 \\ 0, & x^2+y^2=0\end{cases} \]

这一函数沿\(x\)轴和\(y\)轴上的值恒为0，可偏导，但在卦限内部出现了函数值的突变，因此不连续。

---

如果函数可微，则函数在该点处连续。

多元函数可偏导不一定可微。

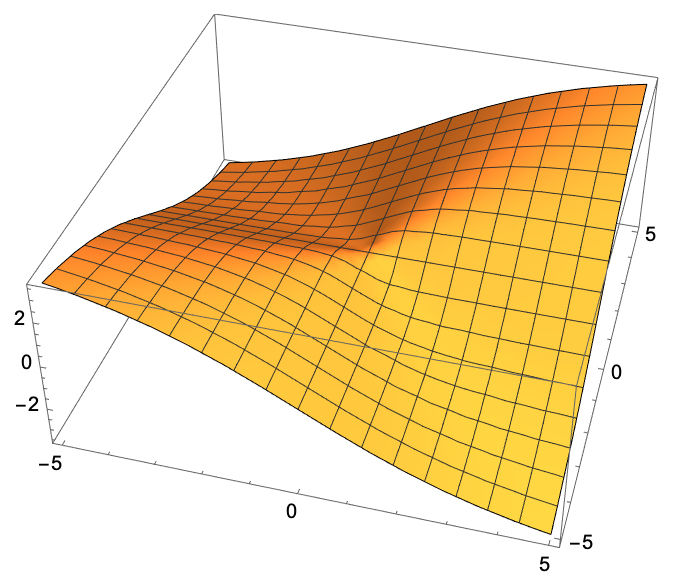
这一函数沿\(x\)轴和\(y\)轴上的值恒为0，但在卦限上有增量。